자율학습에서의 특징 선택

이 블로그 시리즈 1부에서, 우리는 특성 선택이 컴퓨터로 할 수 있는 어려운 문제라는 것을 알았습니다. 그리고 나서 우리는 진화 알고리즘이 제2부에서 이 문제를 다룰 수 있다는 것을 보았습니다. 마지막으로 논의한 바에 따르면 객관적인 최적화를 통해 데이터 및 기계 학습 모델에 대한 추가적인 통찰력을 제공하는 것으로 나타났습니다. 아직 논의하지 않은 한가지가 있는데, 다중 객체 특성 선택입니다. 그것은 또한 자율 학습을 위해서도 사용될 수 있습니다. 이는 이제 클러스터를 찾을 수 있는 가장 좋은 기능 공간도 식별할 수 있다는 뜻입니다. 그 문제에 대해 좀 더 자세히 논의하고 이제 어떻게 해결할 수 있을지 알아봅시다.

자율학습에서의 특징 선택 및 밀도 문제

이 게시물에 대한 클러스터링 문제를 중점적으로 다룰 예정입니다. 아래에 있는 모든 것들은 대부분의 다른 자율학습 기술에도 유효합니다.

일단 k-means 클러스터링에 대해 이야기해 보겠습니다. 알고리즘의 목적은 주어진 수의 클러스터에 대한 중심을 식별하는 것입니다. 이러한 중심은 각 클러스터의 데이터 지점들에 대한 평균입니다. 그런 다음 다시 계산될 모든 데이터 점을 몇 개의 점을 다시 할당한 후에 중심점에 할당합니다. 이 절차는 최대 반복 횟수가 초과되거나 클러스터가 안정적으로 유지된 후에 다시 할당된 점이 없으면 중지됩니다.

그러면 알고리즘이 우리의 데이터를 얼마나 잘 분할했는지 어떻게 측정할 수 있을까요? 이를 위한 공통적인 기법이 있습니다. 즉, Davis-Bouldin 인덱스(즉, DB인덱스)입니다. 다음 공식을 사용하여 계산할 수 있습니다.

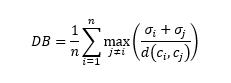
클러스터 숫자로 n을, 클러스터 I의 중심으로 c를, 클러스터 I의 중심으로 모든 점의 평균 거리를 σ로, d(c, c)를 클러스터 i와 j의 중심과 중심 사이의 거리로 합니다.

보시다시피 클러스터 내의 포인트가 서로 근접한 경우 클러스터링 결과가 더 좋습니다. 물론 우리가 원했던 것도 바로 이 때문이지만, 이는 DB인덱스가 클러스터 밀도가 더 높은 클러스터링 결과를 선호한다는 뜻이기도 합니다.

하지만 클러스터에서 밀도를 높이려는 이러한 선호로 인해 특징을 선택하는 데 문제가 있습니다. 특징을 선택하면 특징의 수가 줄어든다. 특징이 작다는 것은 나머지 차수에서 밀도가 높다는 것을 의미하기도 한다. 이는 직관적으로 이해할 수 있는 것이 우리가 고차원적 공간의 데이터 점을 더 작은 차수로 매핑하여 그 점들을 서로 가깝게 하기 때문입니다.

기존의 특징 선택은 클러스터링에 사용할 수 없습니다. 우리가 데이터의 일부로 순수한 노이즈가 존재하지만 완전히 랜덤한 하나의 특징을 가지고 있다고 상상해 보세요. 동전을 던져 0은 앞면 1은 뒷면이라고 해봅시다. k=2의 k-means클러스터링을 사용하여 데이터에서 2개의 클러스터를 찾고 나서 이 작업에 최고의 특징 집합을 찾기 위해 전진선택법(forward selection method)을 사용하기로 결정합니다. 먼저 하나의 특징만 사용하여 최적의 클러스터를 찾으려고 합니다. 물론 위에서 설명한 우리의 랜덤한 특징이 이번 레이스에서 우승할 것입니다. 즉, 무한한 밀도를 지닌 두개의 클러스터를 만들 것입니다! 한 클러스터는 0에서 모든 점을, 다른 클러스터에서는 1에서 모든 점을 가지지만, 이 점이 완전한 랜덤 기능이었다는 점을 생각해야 합니다. 결과적으로, 이 차원만 사용한 클러스터링은 원래 문제와 데이터 공간에서는 완전히 의미가 없습니다.

의사-범주형 랜덤 특징이 없는 경우에도 항상 하나의 특징만 선택합니다. 즉, 가장 밀도가 높은 클러스터를 제공하는 클러스터입니다. 더 많은 기능을 추가하는 것은 밀도를 다시 낮출 뿐이므로 우리는 하지 않을 것입니다.

해결책 : 다중 객체 특징 선택

다중 객체 최적화가 이 문제에 도움이 될 수 있을까요? 실험을 해 보고 어떻게 작동하는지 봅시다. 아래 데이터 셋에는 2차원, 즉 att1과 att2에 클러스터가 4개 있습니다. 또한 random1, random2 등 4개의 추가적인 랜덤 특징이 있습니다. 랜덤 특징은 0 주위의 가우스 분포를 사용합니다. 참고:데이터가 평준화되어 모든 데이터 열이 평균 0 및 표준 편차 1을 갖습니다. 이 과정을 표준화라고 합니다.

이 포스트의 아래쪽에 있는 각 프로세스에 대한 링크를 참조하십시오. 다음은 att1과 att2의 차수만 보는 경우 데이터 셋의 모양입니다.

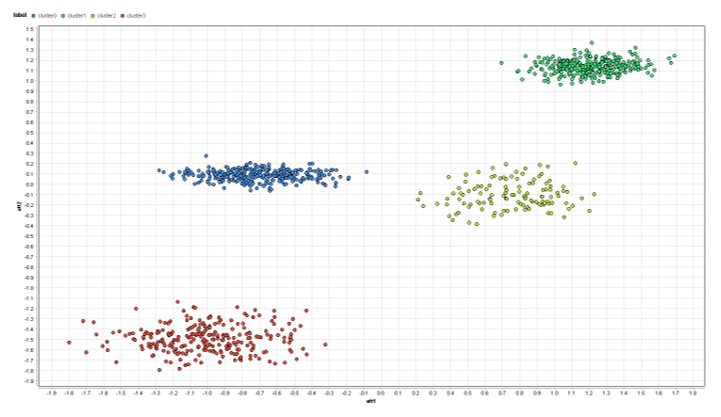
여기서는 4개의 자연스러운 클러스터를 보기가 쉽습니다. 그러나 동일한 점 색을 사용하여 동일한 데이터를 구성하면 약간 변경됩니다. 아래에서는 차수를 random1과 random2를 대신 사용합니다.

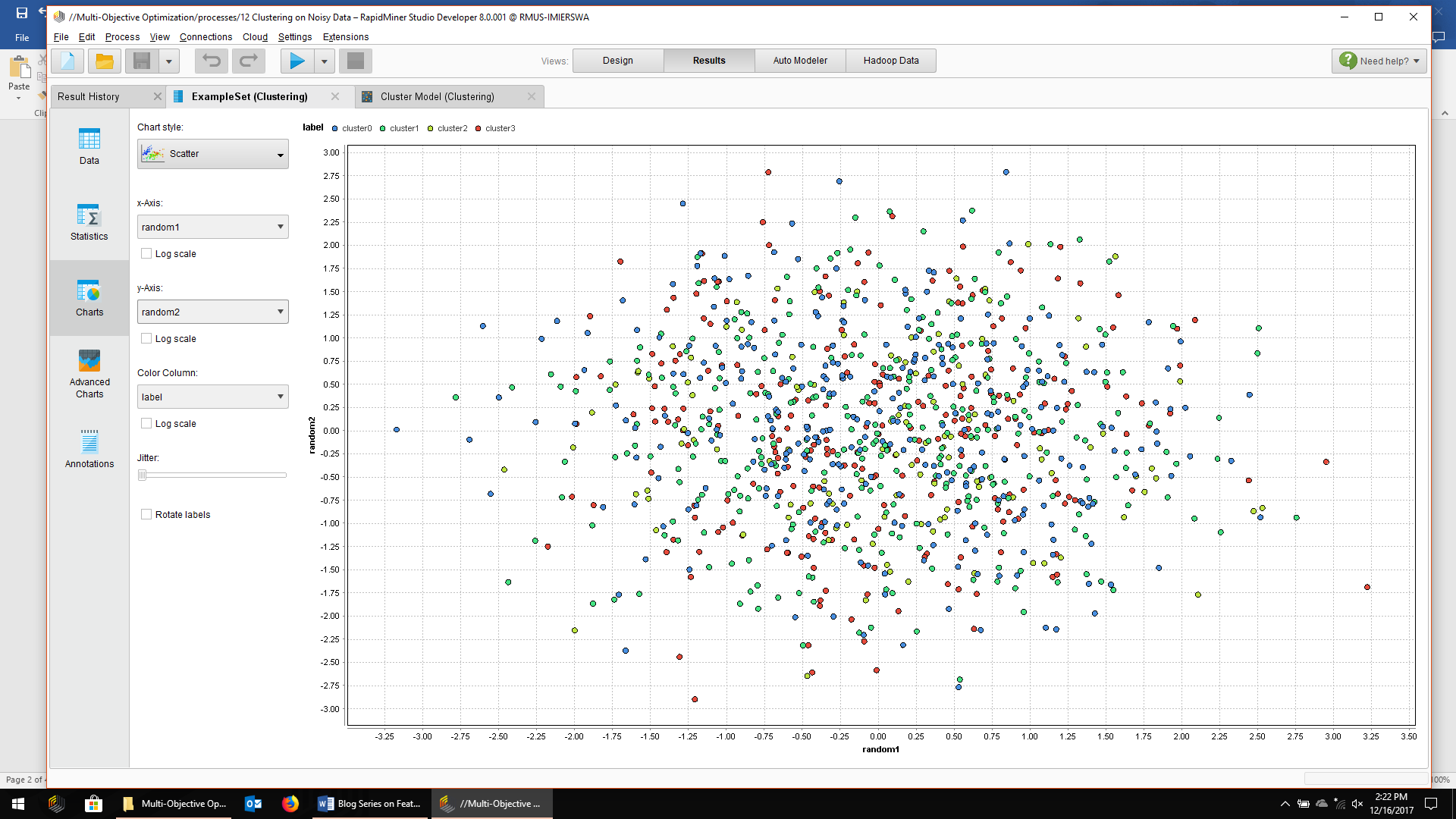
예상대로 더 이상 클러스터를 볼 수 없으며 데이터 지점이 중심에서 랜덤으로 산란됩니다. 특징 선택을 시작하기 전에 6개의 특징으로 구성된 전체 데이터 셋에서 k=4로 k-means클러스터링을 실행하면 됩니다.

이제 클러스터는 k-means가 발견한 클러스터를 나타내며 완전히 끔찍하지는 않습니다. 그럼에도 불구하고, 추가적인 랜덤 특성이 k-means를 사용 못하게 하였습니다. 왼쪽에는 빨간 색과 파란 색 클러스터가 완전히 혼합되어 있으며, 빨간 색과 파란 색 점의 일부는 오른쪽 클러스터에도 있습니다. 오른쪽의 노란 색 클러스터와 녹색 클러스터도 마찬가지입니다.

이러한 노이즈 특성은 클러스터링을 완전히 무의미하게 만들 수 있다는 것을 보여 줍니다. 원하는 클러스터를 찾을 수 없습니다. 기존의 특징 선택은 도움이 되지 않으므로 다중 객체 접근 방식이 얼마나 효과적일지 살펴보려고 합니다.

우리는 이전 포스트와 동일한 기본 설정을 사용합니다. 첫째, 데이터 셋을 검색한 다음 위에서 설명한 대로 데이터를 표준화합니다. 그런 다음, 우리는 선택 계획으로 "특징의 중요성이 없는 정렬(non-dominated sorting)"을 사용하는 진화적 특징 선택 스키마를 사용합니다

.

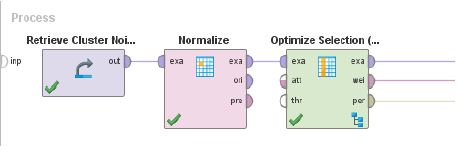
특징 선택 Operator 내부 차이가 약간 큽니다.

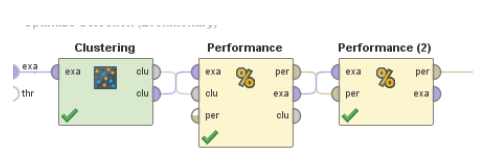
10겹의 교차 검증을 사용하는 대신 k=4를 사용하여 클러스터링을 만들 수 있습니다. 첫 번째 성능 operator는 클러스터링 결과를 가져오고 DB인덱스를 계산합니다. 두번째 operator는 현재 개인에 사용되는 특징의 수를 계산합니다. 우리는 최적화를 위해 이 숫자를 두 번째 목표로 삼았습니다.

이제 이 프로세스를 실행할 수 있습니다. 다음은 30번 이후의 Pareto front 모습입니다.

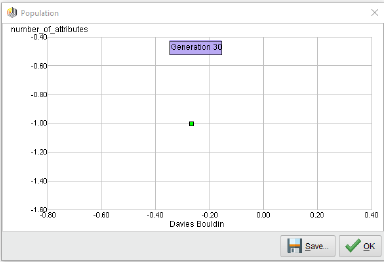
Pareto front에서 하나만? 그렇습니다! 특징 수를 최소화하고 클러스터 밀도를 최적화하려는 특징 선택 체계는 항상 하나의 기능만 제공합니다. Pareto front는 12번를 거쳐 이 단일 지점으로 붕괴했고, 나머지 기간 동안 그 상태를 유지합니다.

선택된 기능이 att2를 선택했으므로 나쁘지 않은 선택입니다. 실제로, 이 차원에서 발견된 4개의 클러스터에 대한 분포를 보여 주는 히스토그램이 표시됩니다.

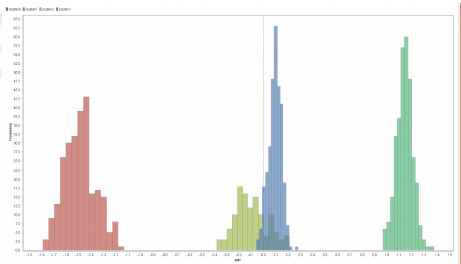
빨강과 초록은 꽤 좋습니다. 하지만 파란 색 클러스터와 노란 색 클러스터는 겹치는 부분이 많습니다. 이 게시물의 첫 번째 이미지를 다시 확인하고 4개의 클러스터를 2개의 컨트롤러에만 투영하면 동일한 결과가 나옵니다.

원하는 클러스터를 얻게 하기 위해서는 특성 att2와 att1이 모두 필요하다는 데 동의하지만, 대신에 기능이 하나만 필요합니다. 다중 객체 최적화만으로는 여기서 도움이 되지 않을 것으로 보입니다. 그 이유는 두 목표가 상충하지 않기 때문에 모든 절충을 보여 주는 Pareto front가 없을 것입니다. 어떤 타협q도 보여 줄 수 없습니다.

여기 한가지 아이디어가 있습니다. 특징의 숫자에 맞게 최적화 방향을 바꾸면 어떨까요? 특징의 수를 최소화하는 것이 상충하지 않는다면, 그 대신에 수를 극대화하기 위해 충돌을 도입하지 않는 이유는 무엇입니까?

처음에는 말도 안 되는 소리로 들릴 수도 있지만, 생각해 보면 이해가 될 것입니다. 클러스터링의 핵심은 데이터를 설명하는 것입니다. 가능한 한 원래의 데이터 공간에 가까이 있으면서 실제로는 쓰레기 값만 생략하는 것이 좋습니다. 생략을 너무 많이 하면 우리의 기술은 더 이상 쓸모가 없을 것입니다. 그것은 마치 당신이 사물을 묘사할 때 너무 많은 세부 사항들을 생략하는 것과 같습니다. "바퀴가 달렸다"는 "자동차"에 대한 잘못된 설명이 아니라 자전거, 오토바이, 심지어 비행기와 같은 다른 많은 것들에도 적용됩니다. 하지만"…의자 4개와 엔진 하나"를 추가하면 불필요한 세부 정보를 너무 많이 추가하지 않고도 이 기술을 훨씬 더 잘 설명할 수 있습니다. 박사 논문에서 우리는 이 아이디어를 "정보 보존(information preservation"이라고 불렀습니다.

실제로 위의 RapidMiner프로세스에서 한가지만 변경하면 됩니다. 두 번째 수행 operator는 "최적화 방향"이라는 창의적인 매개 변수를 가지고 있습니다. 이를 "최소화"에서 “최대화"로 변경하면 이동할 준비가 됩니다. 다음은 이 최적화 실행이 끝났을 때 우리가 얻게 될 Pareto front입니다.

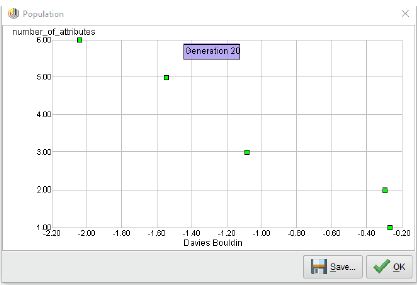
훨씬 좋아 보입니다, 그렇지 않습니까? 우리는 Pareto front에서 5가지 다른 점을 발견했습니다. DB인덱스는 처음 2개의 속성만 사용하고 나머지는 3,5,6 특성을 사용하는 솔루션을 사용하여 분명한 차이를 보입니다. 그렇다면 이러한 최초의 두 솔루션을 특별하게 만드는 것은 무엇일까요? 솔루션에 대한 세부 정보가 포함된 표가 있습니다.

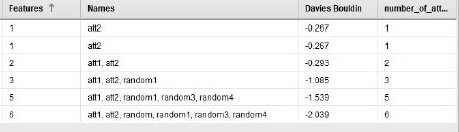
첫째, 하나의 속성만 사용하여 동일한 솔루션을 두 번 사용합니다. 우리는 이미 여기서 att2가 최고의 DB인덱스를 갖고 있다는 것을 알고 있습니다. 그러나, 다음 것은 DB인덱스 측면에서 조금 더 나쁠 뿐이며 또한 att1에 "필수"기능도 추가합니다. 이제부터, 랜덤 기능을 추가하기 시작하면 DB-인덱스가 완전히 하락합니다.

결과 클러스터를 검사하지 않고 클러스터를 최종 선택할 수는 없습니다. 하지만 이제 우리는 그들이 말이 되는지, 그리고 의미 있게 우리의 데이터를 기술하는지는 적어도 알 수 있습니다. DB-인덱스에 대한 명확한 하락 직전에 그러한 영역에서 시작하는 것이 종종 좋은 생각입니다. 이는 클러스터의 최적 숫자 k를 선택하는 알려진 팔꿈치 기준과 다르지 않습니다. 우리는 위의 Pareto front 차트에서 이 하락의 모양을 명확히 볼 수 있습니다.

정보보존 접근 방식은 모든 관련 정보를 제공합니다. 이 정보를 한번의 최적화 작업으로 얻을 수 있습니다. 자율학습을 위한 특징 선택이 마침내 해결되었습니다.

결론

딥 러닝 시대 조차도, 여전히 다른 모델 유형이 우수하거나 선호되는 많은 애플리케이션이 있습니다. 또한 거의 모든 경우에 이러한 모델은 불필요한 기능을 삭제하여 입력 데이터의 노이즈를 줄이는 이점을 누리게 됩니다. 모델은 지나치게 적합한 경향이 덜하고 더 단순해 지므로 작은 데이터 변경에도 더욱 강력해 집니다. 또한 단순함은 모델의 이해하기 쉬움을 향상시킵니다.

진화 알고리즘은 특징을 선택하는 강력한 기술입니다. 그들은 전향적 선택이나 후퇴적 제거와 같은 첫 번째 지역적 최적에 고착되지 않고 있습니다. 이는 더 정확한 모델로 이어집니다.

훨씬 더 좋은 접근법은 다중 객체 선택 기술을 사용하는 것입니다. 이러한 알고리즘은 동일한 런타임에 전체 Pareto fornt 솔루션을 제공합니다. 복잡성과 정확성 사이의 균형을 직접 검사할 수 있습니다.("이 추가 기능을 추가하는 것이 정말 가치가 있나?")기능의 상호 작용에 대한 추가적인 통찰력을 얻을 수 있습니다.

마지막으로, 이러한 다중 객체 특성 선택 접근법은 또 다른 장점을 가지고 있습니다. 우리는 그것을 클러스터링 기술과 같은 자율 학습에 사용할 수 있습니다. 하지만, 우리는 특징의 숫자에 대한 최적화 방향을 변경할 필요가 있습니다. 밀도 기반 클러스터 측정을 극대화할 때 이 점을 쉽게 확인할 수 있습니다. 또한 특징 수를 최소화하는 동시에 단 하나의 특징만 확보할 수 있다면, 특징 수를 극대화할 경우 더 많은 기능을 위한 고밀도 클러스터를 찾기가 더 어렵습니다. 이는 합리적인 수의 모든 기능에 가장 적합한 클러스터로 이어집니다. 또한 클러스터링이 무엇인지에 대한 원래 정보를 보존합니다. 즉, 원본 데이터에서 숨겨진 세그먼트를 찾습니다.

여기에 있습니다. 미래에 필요한 유일한 특징 선택 솔루션입니다.

RapidMiner 프로세스

RapidMiner를 여기에서 다운로드할 수 있습니다. 그런 다음 아래의 프로세스를 다운로드하여 RapidMiner에 직접 이 기계 학습 모델을 구축할 수 있습니다.

zip파일을 다운로드하고 압축을 푸세요. 그 결과"File"->"ImportProcess"를 통해 RapidMiner에 로드할 수 있는 .rmp 파일이 생성됩니다. 다른 프로세스에서 사용될 데이터 세트를 생성하려면 처음 3개의 프로세스를 실행해야 합니다. 설정에 따라 모든 프로세스의 저장소 및 검색 operator 매개 변수에서 저장소 경로를 조정하세요.